Maxwell: Las funciones colorimétricas del ojo humano

El triángulo de Maxwell

En su ensayo de 1860 On the Theory of Compound Colours, and the Relations of the Colours of the Spectrum, James Clerk Maxwell informó de lo resultados de sus experiencias en la clasificación de los colores con un disco giratorio cinco años antes.

Aunque Helmholtz la había rechazado en 1852, Maxwell insistió en la veracidad de la teoría de los tres receptores de Thomas Young como base biológica de la visión de los colores. Concebía los tres colores fundamentales de Young como vértices de un triángulo plano que contenía todos los colores espectrales.

La idea de Maxwell era que fijando tres colores —a los que él llamó estándares— en el diagrama de Newton y usando la regla del baricentro, se podrían calcular todos los colores que sean una mezcla de cantidades dadas de esos tres colores estándares y por tanto se puede construir una forma triangular —que en adelante llamaremos 'triángulo de Maxwell'— del diagrama de Newton o, en otras palabras, construir una primera aproximación con forma triangular del círculo de Newton.

De hecho, según destacó Maxwell, también se puede construir la parte del diagrama situada fuera de ese triángulo. Para hacer coincidir el baricentro con un punto externo, uno o dos de los pesos deben ser negativos. Esto, a pesar de seguir los principios matemáticos, no tiene una interpretación física directa, ya que no es posible mostrar un peso negativo.

Sin embargo, Maxwell especificó también los colores exteriores al diagrama y halló así una forma más precisa del diagrama cromático, que Newton, en una primera aproximación, había dibujado en forma de círculo.

En lo que respecta a los colores estándares, Maxwell eligió rojo bermellón, verde esmeralda y azul marino.

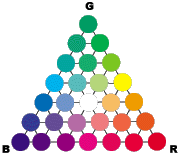
Maxwell fue pues el primero en establecer con medidas efectivas el diagrama circular de Newton. Su trabajo permitió dar a cada color —que estuviera en el interior del triángulo— dos coordenadas basadas en tres colores estándares elegidos. La elección de colores estándares es todavía libre, en el sentido de que cualquier triada de colores es válida —siempre que ninguno de los tres se pueda obtener a partir de una mezcla de los otros dos—. Con unos simples cálculos se puede pasar de las coordenadas de un color dado en términos de una triada a los datos en términos de otra triada.

El disco giratorio

El experimento de Maxwell descrito en el artículo de 1860 era en realidad la síntesis final de una serie de experimentos efectuada anteriormente con círculos giratorios coloreados y posteriormente con luces de colores.

En su primer trabajo sobre la teoría de los colores, de 1855 y habiendo perfeccionado el disco de colores inventado por Thomas Young, Maxwell expuso el hecho ya descrito por Helmholtz de que la mezcla aditiva de colores se puede conseguir con luces que se superponen o con círculos con sectores de colores que giran velozmente. En ambos casos, los colores se funden la retina del ojo. Es decir, estableció que todos los colores del espectro se podían obtener sumando proporciones adecuadas de tres colores primarios (rojo, verde y azul).

Maxwell hizo construir unos circulos de colores de modo que dos o más se pudieran entrelazar entre si y la relación y proporción entre las superficies de dos o más colores se pudiera determinar con facilidad.

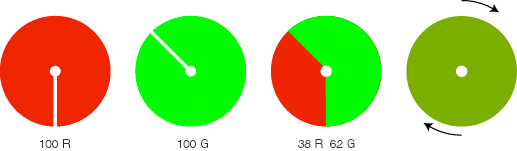
Con este aparato es posible realizar la síntesis aditiva de dos o más colores.

Llegados a este punto, se puede intentar realizar las distintas síntesis aditivas de los tres colores estándar elegidos y confrontarlas a un cuarto color realizado en el centro del disco. pare ello se hace lo siguiente:

Tras haber colocado los discos de estos tres colores sobre el plato circular del dispositivo giratorio y los discos más reducidos de blanco y negro encima de ellos, el experimentador debe hacer girar el plato y pedir la opinión de los observadores sobre la relación entre el anillo externo y el círculo interno.

En cada caso, dirá que el círculo exterior es demasiado rojo, azul o verde, y que el interior es demasiado claro u oscuro respecto al exterior. Entonces, se harán ajustes sucesivos en la forma de representar el color en el círculo exterior para que se perciba como lo más cercano posible al del interior. Una vez hechos estos ajustes, los colores del círculo exterior e interior deben ser totalmente indistinguibles cuando el plato tenga una velocidad de giro suficiente.

Entonces, se debe leer la cantidad de divisiones espaciales en los distintos sectores de colores en el borde exterior del plato y expresarlo en forma de ecuación. Los números obtenidos en un experimento con colores citado arriba y realizado el 6 de marzo de 1855 a la luz del día —sin sol— son:

0,37 Rojo + 0,36 Verde + 0,27 Azul = 0,28 blanco + 0,72 negro

Maxwell demostró que estas correspondencias de colores se pueden expresar como ecuaciones de color que a su vez se puede manipular con coeficientes negativos, como si fueran posibles intensidades negativas. Estas ecuaciones permiten localizar sobre el plano cualquier color, en relación con los otros tres colores fijos y representarlos en el plano. En particular, es posible localizar los colores espectrales, lo que constituye un problema exclusivamente experimental.

Para las medidas de 1860, Maxwell uso un aparato distinto de su invención, la caja de colores, en la que consiguió mezclar directamente los rayos de colores obtenidos de la descomposición de la luz solar mediante prismas.

Maxwell comenzó eligiendo tres estímulos primarios —bien distanciados en el espectro—, tres radiaciones monocromáticas con las siguientes longitudes de onda:

R = 630,2 nm. (rojo) G = 525,1 nm. (verde) B = 456,9 nm. (azul). [Las iniciales RGB, que se usan corrientemente, corresponden a Red (rojo), Green (verde) y Blue (azul) del inglés, respectivamente.]

Además, definió una radiación blanca apropiada para definir la unidad de medida de las radiaciones primarias.. Una unidad de rojo, una de verde y otra de azul dan como resultado blanco.

En un artículo anterior, Maxwell justificó la elección de los tres primarios afirmando:

Si se hubiese elegido rojo, azul y amarillo sería difícil formar el verde como mezcla compuesta por azul y amarillo, mientras que el amarillo formado con el rojo bermellón y el verde esmeralda es bastante distinto.

Para cada una de las tres radiaciones monocromáticas —diferentes en los tres primarios—Maxwell igualaba una mezcla de esas radiaciones más el blanco con una mezcla de dos de las tres radiaciones primarias.

Con las mediciones se obtienen trece ecuaciones, de las que éstas son las dos primeras:

44,3 F1 = 18,6 R + 0,4 G + 2,8 B
16,1 F2 = 18,6 R + 5,8 G + 0,1 B

A partir de estas trece ecuaciones, Maxwell obtuvo la primera realización numérica del espacio del triestímulo basada en observaciones experimentales.

Recordemos que el baricentro de los tres pesos r, g y b aplicado a los puntos R, G y B está en el interior del triángulo RGB. Para calcularlo se puede empezar por calcular el baricentro M de los dos primeros pesos r y g, y después el baricentro de aplicado en M y b.

Alternativamente, se puede fijar en el interior del triángulo —que Maxwell ideó equilátero— un sistema de coordenadas triangulares. En este sistema, cada punto en el interior del triángulo, tiene tres coordenadas (x, y y z) de modo que x+y+z = constante —por lo que sólo es necesario especificar dos—. Con este sistema de coordenadas, el baricentro de los tres pesos r, g y b, situados respectivamente en R, G y B, tienen las coordenadas:

x = r / (r+g+b)
y = g / (r+g+b)
z = b / (r+g+b)

Tomando entonces r a partir del rojo, g a partir del verde y b a partir del azul, el color resultante se sitúa en un punto interior del triángulo (o sobre uno de sus ladois) que es el baricentro de los tres pesos r, g y b situados en R, G y B. Al color resultante se le pueden asignar las coordenadas x, y y z o, más sencillamente, sólo dos de ellas, ya que la suma de las tres es constante.

Los colores son vectores

Para introducir una tercera dimensión, hasta entonces tratada sólo de forma implícita mediante los pesos, Maxwell desarrolló la idea de Grassmann de hablar de vectores.

Consideremos el plano en el que se sitúa el triángulo y el consiguiente diagrama cromático. Establezcamos que en este plano la intensidad de los colores sea igual a 1. Tomemos un punto O como origen, situado fuera de este plano. Una línea que una el origen con un punto cualquiera del triángulo tiene una dirección que depende de la posición del color en el diagrama y, por tanto, podemos considerarla representativa del color correspondiente.

Para indicar la cantidad, la prolongamos más allá del plano en la misma relación en la que se supera la unidad. Para otra cantidad dada de colores, se define un plano paralelo más cercano o lejano al origen. Los puntos de intersección de estos planos con un vector determinado constituyen un color, y el plano al que pertenece determina la luminosidad. Esto vale para todos los colores en el interior del triángulo, en su exterior y también sobre el borde, incluidos los colores estándar.

Establecido este sistema, el resultante de dos colores se puede calcular con la regla del baricentro de Grassmann.

Sea una sección AB del plano del diagrama donde OP y OQ representan colores, con las cantidades de P y p = OP/OA y de Q y q = OQ/OA. La resultante se representa como C, donde AC:CB = q:p y la cantidad es p+q, así que OR = OC(p+q).

Cada vector representa pues un color con una luminosidad que parte de 0 al origen, y que es 1 cuando intersecta con el plano, volviéndose siempre más intenso conforme a su distancia al origen.

De este modo, cualquier color de la naturaleza se puede representar, sea en cualidad o cantidad, en algún punto de este espacio de colores.

Podemos expresar la posición de cada punto en el espacio si establecemos un conjunto de tres ejes de coordenadas. Este sistema de tres coordenadas es un ejemplo de la tridimensionalidad del color, una reformulación de la primera ley de Grassman.

En este punto, todo estaba dispuesto para determinar la posición de los colores del espectro en este espacio y, por tanto, con relación al triángulo de Maxwell y el diagrama de Newton.