Diagrama de cromaticidad

Aparte del valor del triestímulo Y, que es el correlato del atributo del brillo, los otros dos valores del triestímulo X y Z no se corresponden con ningún atributo perceptual.

Sin embargo, algunos atributos perceptuales del color son correlatos de magnitudes relativas, no absolutas, de los valores del triestímulo. Las magnitudes relativas se calculan con estas fórmulas, que definen las coordenadas de cromaticidad de un valor cuyos valores de triestímulo sean X, Y y Z:

x = X / (X + Y + Z)

y = Y / (X + Y + Z)

z = Z / (X + Y + Z)

Por ejemplo, si X = 8, Y = 48, Z = 24, entonces X+Y+Z = 80 y x = 8/80 = 0.1; y = 48/80 = 0.6; z = 24/80 = 0.3. Esto significa que este color en concreto contiene un 10% de x, un 60% de Y y un 30% de Z. Como x se corresponde de modo aproximado al rojo, y al verde y z al azul, se puede pensar que se trata de un verdeazulado de un factor de luminancia Y a mitad del blanco y el negro.

Como x + y + z = 1, se deduce que son suficientes dos de los valores colorimétricos relativos; en la práctica los dos utilizados son x e y. Con estos dos valores es posible construir un diagrama bidimensional como el siguiente.

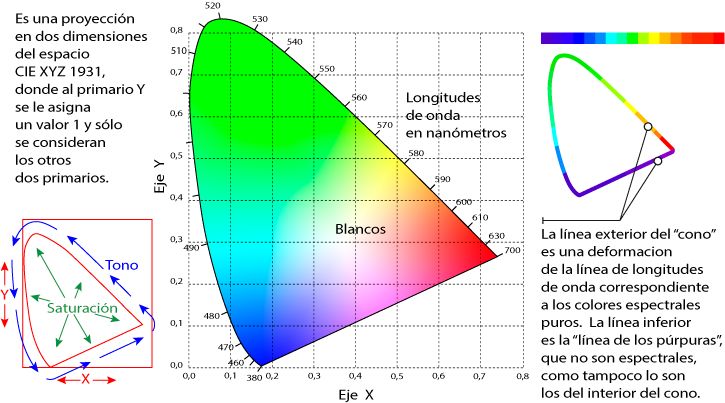
¿Qué representa este diagrama? Consideremos todos los valores del triestímulo XYZ que tienen los mismos valores relativos xyz. Todos estos valores del triestímulo difieren entre si sólo por su luminancia. Todos estos valores del triestímulo difieren entre si sólo por un coeficiente multiplicativo y, por tanto, representan colores que sólo se diferencia por la luminancia. De ello se deduce que todos estos colores tienen la misma cromaticidad. El diagrama de arriba representa, por tanto, la cromaticidad y es por esto por lo que se denomina diagrama de cromaticidad (chromaticity diagram).

Este diagrama proporciona un diagrama de toda la cromaticidad, es decir, de todos los colores descontando la luminancia. La linea curva del diagrama indica el límite espectral posible (spectral locus) y la línea recta es la línea del púrpura (purple boundary). Las coordenadas x e y asumen valores que van de 0 a 1.

Por tanto, es posible representar un color con los distintos valores del triestímulo XYZ o con los valores de luminancia y cromaticidad Yxy. Si se conocen estos últimos, X y Z se obtienen con las fórmulas:

X = x Y / y

Z = (1 – x – y) Y / y

El diagrama de cromaticidad tiene una importante función didáctica porque permite ilustrar las zonas para las que los primarios de la sintesis aditiva se han elegido en la zona del rojo, del verde y del azul y las regiones para las que los valores del triestímulo, si los primarios son colores reales (es decir, si están dentro del diagrama), pueden ser negativos. Los tres primarios imaginarios que dan origen al diagrama CIE 1931 tienen coordenadas de cromaticidad x e y iguales a (1,0), (0,1) y (0,0), respectivamente.

Por otra parte, hay que subrayar que la representación del diagrama que ilustra esta página es aproximada ya que no es posible ni imprimir ni reproducir toda la cromaticidad con los aparatos y sistemas disponibles. Como veremos, cada dispositivo (sobre todo de impresión) sólo es capaz de reproducir una parte de la cromaticidad.