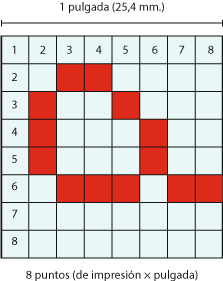
En la actualidad, las máquinas electrónicas destinadas a la impresión sólo tienen un sistema de imprimir: Dividen el espacio imprimible en una retícula de diminutas celdillas y imprimen unas sí y otras no.

Al espacio mínimo imprimible, cada una de las celdillas de la retícula en las que las máquinas dividen el espacio, se le denomina punto (de impresión). Ese término "punto" es un poco ambiguo y da lugar a algunas confusiones entre punto de impresión y punto de trama.

En la imagen superior vemos un ejemplo: Siete puntos de impresión dentro de una retícula de 20 × 20 puntos de impresión. Si esta retícula tuviera 1 pulgada de lado, la resolución del aparato sería de 20 puntos por pulgada.

Los procedimientos pueden variar. Los fluidos que se aplican y los medios sobre los que se aplican, también, pero lo que no varía, por lo menos a comienzos del siglo XXI, es el hecho de que las máquinas sólo pueden imprimir un punto o no imprimirlo. No pueden "imprimirlo un poco", como sí haría un pincel o un lápiz manejado por un artista.

Antes de entrar en materia, hay que destacar que los aparatos a los que aquí se hace referencia son básicamente aparatos PostScript, que es el sistema para la realización de documentos digitales predominante hoy día en las artes gráficas.

Una máquina capaz de dividir un espacio dado en más celdillas que otra, hará que estas celdillas sean más pequeñas. El resultado de esto será que el dibujo que trace imprimiendo unas celdillas sí y otras no, será mucho más detallado.

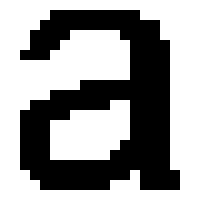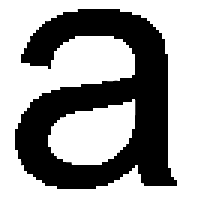Una letra formada con muy baja resolución. Está dentro de una retícula de sólo 20 celdillas lineales.	La misma letra con mayor resolución (una retícula de 66 celdillas lineales). El detalle es mejor.	Y la retícula es ahora de 200 celdillas lineales. El dibujo es más complejo y nítido.

El número de celdillas o unidades mínimas de impresión que una máquina es capaz de realizar como máximo en un espacio dado es lo que se llama "resolución". A mayor número de resolución, mayor nitidez de dibujo.

Es importante resaltar que la resolución se suele medir en puntos por pulgadas (abreviado en español como ppp) y que estas son siempre lineales, es decir, que están formadas por una fila de puntos de impresión colocados en línea, uno detrás de otro. Así, hablamos de una impresora con 300 puntos por pulgada (una pulgada equivale a unos 2,54 centímetros).

De hecho la resolución en puntos de impresión por pulgada cúbica de una filmadora de 2.400 ppp es de 5.760.000 puntos, la resolución por pulgada cúbica de una impresora de 600 ppp es de sólo 360.000 puntos. La diferencia es notable (por eso los fabricantes de impresoras han logrado imponer la medida lineal sin resaltar la palabra "lineal", la diferencia parece menor...).

A cualquier sistema que se base en la división del espacio en una retícula, se le puede aplicar este concepto de "resolución". De hecho, los monitores tienen una resolución de 72 píxeles por pulgada en los aparatos Macintosh y 96 píxeles por pulgada en los PCs del sistema Windows. Incluso se puede hablar de resolución al hablar de alfombras persas (de hecho, se hace así y se habla de "nudos por centímetro", cuantos más nudos, mejor calidad de dibujo y mayor precio).

Resolución, porcentajes de tinta e impresión de imágenes

• En Los textos e imágenes de línea

  Al 100%, sin tramar

  Cuando una máquina tiene que imprimir una línea, una forma cualquiera o ima imagen de línea (es decir: una imagen de mapa de bits de 1 bit de profundidad) al 100% de la tinta —o tintas— que tiene a su disposición, no tiene problemas, lo hace a la máxima resolución que se le haya ordenado dentro de sus límites de fabricación.

  Así, un texto o un dibujo de línea que se impriman al 100% de tinta —ya sea negra, magenta o cualquier otra— en una maquina capaz de 2.400 ppp., imprimirá dichos textos e imágenes a 2.400 ppp., puros y duros —salvo que se haya especificado por algún motivo que lo haga a una resolución menor (modo "borrador" o algo similar)—.

  Por eso, si queremos reproducir óptimamente una imagen de línea, deberíamos situarlo (al 100% de tamaño de reproducción) con la misma resolución de impresión que el dispositivo que la vaya a imprimir: Una filmadora capaz de 2.400 ppp debería recibir imágenes de línea de 2.400 ppp…

  …Bueno, no realmente. La verdad es que el ojo humano, en una imagen de línea, no llega a percibir más detalles por encima de los 1.200 ppp. De hecho podríamos decir que, dependiendo del tipo de impresión, con 800 ppp de límite iríamos bien servidos en la mayoría de los casos.

  Cuando hay tramados

  Al intervenir la trama, la cosa cambia. Los objetos e imágenes de línea pasarán a ser impresos como objetos tramados. La trama que la máquina les aplicará será aquella que tenga especificada por defecto para esas situaciones al máximo posible (a no ser, y esto es esencial, que en el programa del fichero original se haya especificado algo concreto).

  En una grabadora de planchas (CTP) o filmadoras —aparatos con resoluciones muy altas, por ejemplo: 2.400 puntos de impresión por cada pulgada—, se habrá especificado una lineatura (linescreen) para el tramado, digamos por ejemplo, de 150 línea por pulgada (lpp). El aparato tratará de hacer semitonos dividiendo el espacio del siguiente modo:

  "Si dispongo de 2.400 puntos de impresión por cada pulgada y me piden que haga 150 líneas de semitono por cada pulgada, eso me da —dividiendo resolución por lineatura— una capacidad de 16 puntos de impresión para cada punto del semitono. Podré establecer 256 gradaciones de tono en cada tinta (puesto que una celdilla de semitono de 16 ×16 da la posibilidad de 256 combinaciones para ese punto de semitono)".

  El resultado de estos cálculos será que la máquina hará todo aquello que le hayamos pedido con un 50% de magenta utilizando esa trama de semitonos así calculada. Si le hubieramos especificado una forma de punto especial (elipse, redondo, cuadrado, línea, etc… ) esa sería la forma del punto que usaría.

  Así se imprimirá una "a" con una tinta al 100%.	Y así se imprimirá con una tinta al 50%.

  Ahora bien, ¿qué ocurrirá con los puntos de semitono en aquella zona del contorno? ¿Se imprimirán enteros, no se imprimirán o se imprimitán a medias?

  La respuesta es algo muy similar a "se imprimirán a medias". En principio, al ser una impresión postscript, la máquina calculará el contorno del objeto y luego la rellenará con una trama del porcentaje adecuado. Esta trama se recortará de la forma más precisa posible allí donde se halle el contorno de un objeto, incluso si este sólo fuera una línea (en cuyo caso, no hablamos de "relleno", sino de "trazo").

  Una vez más, cuanto mayor sea la resolución de la máquina, con mayor nitidez se podrá hacer este "recorte" y más definido se mostrará el objeto, aunque sea aun objeto de trama de semitonos. Este es un punto crucial que distingue objetos vectoriales con un tono de color y objetos de trama de semitono: En aparatos de alta calidad, el contorno de los primeros es extremadamente más nítido que el de los segundos: La trama y sus saltos son menos evidentes.

• En Las imágenes de mapa de bits (semitonos de imagen)

  Como ya hemos indicado, al tramar, los dispositivos aplican la trama y lineatura que tengan especificada como predeterminada al máximo posible (a no ser, y esto es esencial, que en el programa del fichero original se haya especificado algo distinto).

  La resolución ideal de una imagen de semitono

  Una imagen de semitonos ya tiene una resolución por si misma, es una tabla de celdillas llamadas "píxeles".

  

  En un mundo ideal, la perfecta reproducción se conseguiría con un píxel de información para formar cada punto de semitono —una relación 1:1 entre píxeles y puntos de semitono— ni más ni menos. Esa relación, además ahorrará muchos cálculos al RIP y facilitará la impresión de la imagen.

  

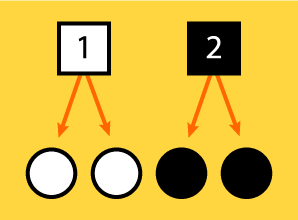
  En el mundo real, los problemas empiezan a aparecer cuando para formar nuestros puntos de semitono no tenemos al menos esa relación de un píxel por punto de trama. Si falta información, la máquina la repite. Es la llamada "pixelización": El uso de un mismo pixel para dos puntos (o más) de semitono.

  Aparecerán los temibles bordes dentados en los contornos de la imagen (inglés: jaggies) y se verán cuadraditos formando la imagen impresa.

  La imagen aparecerá pixelizada porque el RIP no tendrá datos de imagen suficientes para formar esa imagen de calidad ideal de un píxel por punto de trama. En algunos dispositivos que dispongan de un RIP verdaderamente bueno, éste puede hacer una cierta interpolación y "deducir" los píxeles faltantes, promediando los de la vecindad (del mismo modo de que puede hacerlo Photoshop). Ahora bien, esto no "inventará" los píxeles que falten, sólo los fingirá.

  

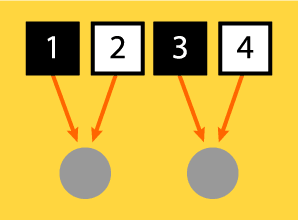
  También existe el fenónemo contrario: Que haya más de un píxel para cada punto de semitono. Eso no es grave pero si molesto a partir de cierta cantidad.

  En ese caso, el intérprete de tramado (RIP) de la máquina promediará los valores de los píxeles participantes y darle el valor resultante al punto de semitono en cuestión. Eso provoca valores "intermedios" que pueden provocar cierta "borrosidad" o suavidad en la transición de zonas de distintos tonos o luminosidad.

  Llegamos a la pregunta clave: ¿Cómo saber cual es la resolución que nos asegura al menos un pixel por cada punto de semitono? ¿Existe una forma de saberlo?

  Pues sí. En principio es simple: Si vamos a imprimir una imagen a una lineatura de 100 lpp, esto quiere decir que en una línea recta habrá 100 puntos de semitono. Entonces bastaría una imagen con una resolución de 100 ppp. Ahora bién, este cálculo presupone que las tramas tienen un ángulo 0. Es decir, que no están tumbadas. Pero en la vida real sabemos que las tramas deben girarse para que su presencia sea poco evidente al ojo. La trama que más girada está con respecto al ángulo 0, es la negra (el color más oscuro y el más evidente al ojo). La trama menos girada es la amarilla (cuya presencia es de por si poco evidente, de hecho está en grado 0).

  

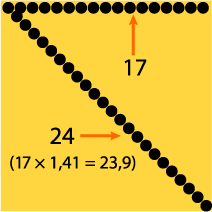
  De ese modo, la trama negra forma la diagonal de ese cuadrado de 100 lpp y mide, obviamente algo más. Ese algo es fácil de saber, ya que (matemáticas de primaria) la diagonal de un cuadrado es igual al lado por la raiz cuadrada de 2. Entonces, para asegurarnos esa relación pixel-trama de 1:1 debemos multiplicar la lineatura (el lado del cuadrado formado por una pulgada) por la raiz cuadrada de 2 (que es aproximadamente 1,41). En nuestro ejemplo sería: 100 × 1,41 = 141 ppp (redondeamos si queremos a 150 ppp.

  Mitos, mitos, mitos…

  ¿Y entonces, porqué muchas personas dicen "el doble de la lineatura" o "300 ppp" a piñón fijo?

  Si preguntas a la mayoría de las personas relacionadas con las artes gráficas "¿Cuál es la resolución necesaria para imprimir una imagen?", la mayoría te responderá: "El doble de la lineatura"… —En nuestro ejemplo eso significaría 200 ppp— y eso cuando no te dicen mecánicamente "300 ppp".

  ¿Exceso de peso? Un ejemplo: un fichero TIFF sin comprimir de tamaño DIN A3 en escala de grises pesa unos 7,38 Mb. a 200 ppp, y 4,15 Mb. a 150 ppp.

  ¿Cuál puede ser la razón de la respuesta de "el doble de la lineatura"? Pues, creo que hay varías. La primera y, desgraciadamente, la más usual es pura y simple rutina aprendida, pereza profesional o curarse en salud ante posibles fallos ("asegurate, que si hace falta ya menguaremos").

  Sin embargo, existen personas que sabiendo muy bien lo que hacen (y reconociendo el valor de la regla anterior) siguen afirmando que en algunos casos sí es necesario un valor del doble de la lineatura. Veamos porque se mantiene en esos casos esa afirmación:

  Hay quien dice que hay dos casos básicos en los que sí es conveniente que las imágenes tengan el doble de la lineatura:

  1. Cuando la lineatura es "gruesa" (por debajo de 133 lpp) como en los periódicos. Quien dice eso, afirma que ese factor asegura que cualquier fallo que pudiera haber de alineación de trama quedará "escondido" por esos píxeles extra que evitarán la aparición de dentados.

  2. Cuando el sujeto o tema de la imagen tiene un detalle extremadamente marcado y sutil y este detalle es muy relevante (fotos de arquitectura, imágenes con líneas muy diminutas y cambiantes: pelo, joyas muy trabajadas, etc… ) La defensa del doble de la lineatura se basa en el mismo principio que antes: Doblar los píxeles asegura que ese detalle se mantendrá siempre y que no aparecerán dentados. Las transiciones serán suaves.

  La verdad es que un servidor no puede decir por sí mismo si estas dos afirmaciones son o no verdad, pero lo cierto es que las fuentes que lo afirman me parecen dignas de crédito, sobre todo en el segundo caso. Personalmente elijo hacerles caso y trabajar con la regla de 1,5 siempre que no sean imágenes con un gran nivel de detalle que vaya a reproducir con un soporte de gran calidad. En el caso de imágenes en lineaturas muy bajas… No sé, ante la duda (y dado que no serán cosas muy grandes) prefiero ser prudente y creer que salvo que sean cosas poco detalladas, también merece la pena trabajar al doble de la lineatura.

  Todo este asunto es algo confuso y, a veces, parece más cuestión de fe que otra cosa. Dicho lo cual, debe quedarte claro que cualquier cosa por encima del doble de la lineatura no aumentará en absoluto la calidad o el detalle de tus imágenes (eso sí te lo puedo afirmar taxativamente). Lo único que tendrán es más píxeles, lo que sobrecargará los cálculos que tiene que hacer el procesador encargado de la impresión y puede perjudicar la calidad de los semitonos resultantes.

La confusión de la resolución

Como se puede deducir de todo lo expuesto más arriba, uno de los problemas principales en este tema es la confusión que existe entre "resolución de impresión", "resolución de semitono" y "resolución de un archivo digital" —equiparable muchas veces a "resolución de escaneado"— . Veamos la diferencia resumida:

1. Resolución de impresión

   Ya hemos visto que es la capacidad máxima de discriminación que tiene una máquina de impresión. Se suele medir en puntos por pulgada líneal.

2. Resolución de trama o semitono

   La capacidad máxima de imprimir una trama con tonos de gris diferentes hasta un máximo de 256. Se debe medir en líneas por pulgada, por lo que se le suele denominar "lineatura" (linescreen). Se halla mediante la simple fórmula de dividir la resolución máxima de impresión de la máquina en cuestión por el número de tonos que se quieren obtener.

3. La resolución de los archivos digitales o de escaneo

   Es el número de píxeles distintos que por unidad de medida lineal (normalmente pulgadas) tiene una imagen. Un archivo con 300 píxeles (ppp: píxeles, que no puntos) por pulgada tiene mayor resolución que uno de 150 ppp. En buena ley, el escaneo se debería medir en "muestras por pulgada" (en inglés samples per inch, spi), pero esto no lo hace nadie.

Las limitaciones en la elección de la resolución

Lo que a estas alturas debes estarte diciendo es algo como: "Bueno, si sé cuánta resolución es capaz de dar un aparato tanto en línea como en trama, lo que debo hacer es dar siempre el máximo y un poco más y curarme así en salud". Esto, que parece lógico, tiene sus problemas.

El primero es que los ficheros grandes tardan más en ser procesados por un RIP (Raster Image Processor, el procesador de ficheros gráficos imágenes de un aparato postscript).

Cuando hablamos de los ficheros EPS de nivel profesional que una impresora o filmadora puede llegar a recibir estamos hablando de cosas verdadermanente grandes. Cualquier ahorro sensato de tamaño es algo que redundará en trabajos manejables y menos dados a causar problemas y retrasos.

El segundo problema es que la lineatura no es algo que podamos elegir al azar. Si mi filmadora es capaz de llegar a las 175 lpp puede ser muy posible que yo no pueda usar ni de lejos esa finura de punto. El limite lo marca el medio en el que vayamos a imprimir, el método que vayamos a usar para ello y el dinero que estemos dispuestos a pagar por ello.

Papeles malos (el típico papel prensa de un periódico, por ejemplo) raramente pueden superar las 100 lpp y suelen rondar las 80 lpp. La razón es que son papeles muy porosos y absorbentes, donde la tinta tiene una ganancia de punto muy elevada que hace que puntos de trama muy pequeños produzcan semitonos de aspecto sucio y empastado. En ese tipo de soportes da mucho mejores resultados una trama más basta, ya que produce semitonos mucho más limpios y nìtidos.

Calidad: El "peso" sólo vale para las dietas

"¿Dos megas son suficientes?": Esta es la típica pregunta de una persona que no anda muy ducha en el tema de la impresión digital y necesita saber si un archivo es lo bastante bueno para ser impreso. El error básico que se esconde tras esta pregunta es confundir la cantidad de píxeles que tiene una imagen (su peso) con los requisitos imprescindibles para tener la calidad necesaria. De forma extremadamente resumida, esos requisitos son:

1. Que el original (digital o no) sea lo bastante bueno de por sí para que la imagen sea suficientemente bueno. Los detalles de este punto están más allá del tema de esta página.

2. Si es un original no digital, que se haya digitalizado en un aparato lo bastante bueno. Dicho de otro modo: El escáner de tu casa no basta para un trabajo destinado a la impresión profesional, aunque en tu monitor se vea bien. Si no eres un profesional del escaneado (y, no te engañes, si lo fueras no estarías leyendo estas líneas), lo mejor es que recurras a los servicios de un buen servicio de escaneado. La calidad suele compensar el precio (cuando se trata de buenos originales, claro). Lo demás vale simplemente como imágenes de referencia para maquetar o similares (en inglés: FPO — for position only— ).

   Si se trata de una cámara digital, estamos en las mismas incluso si hablamos de hacer una simple reproducción.

3. El usuario del escáner o de la cámara deben ser lo bastante profesionales como para obtener una buena fotografía o un buen escaneado. Explicar porqué es innecesario pero es obvio que un mal fotógrafo que no sabe iluminar, enfocar o componer una imagen, no hace una buena imagen.

4. Que el creador de la imagen no se haya dedicado a mejorar la imagen hasta dejarla más allá de toda esperanza. El tratamiento digital de imágenes es una técnica laboriosa que requiere un aprendizaje paciente. No hay que fiarse de los resultados espectaculares en pantalla que se consiguen a los pocos ensayos. Las buenas noticias son que la paciencia en el aprendizaje se ve siempre recompensada por una notable mejora en la calidad.

5. Que seas una persona prudente y previsora. Pregunta a tu impresor o a tu cliente los datos necesarios (lineatura, resolución usual, tamaños de imágen, tipo de flujo de trabajo — RGB con gestión de color, CMYK puro y duro, etc…— ). Si hiciste un escaneado de calidad, y luego retocaste el original, adjunta ese escaneado o el original con una indicación de lo que es. Adjunta también una prueba impresa de lo que quieres y haz las anotaciones necesarias (concisas y claras, no seas ambiguo). Puede que la fotomecánica (por un modico precio) consiga hacer lo que tu querías y no tuviste la capacidad de lograr.

6. Que preguntes, preguntes, preguntes. Lo que te dejes en el tintero ahí se quedará para la próxima vez (y toma notas, que escribir no daña).